If you hang around causal folks for long enough, you’ll probably hear a version of the sentence: “you can’t just run a regression on observational data” sooner or later. Is that really true? Statisticians (and other scientists) have been running regressions for a very long time, surely it can’t be that bad? Let’s have a closer look!
Two stories
A first example
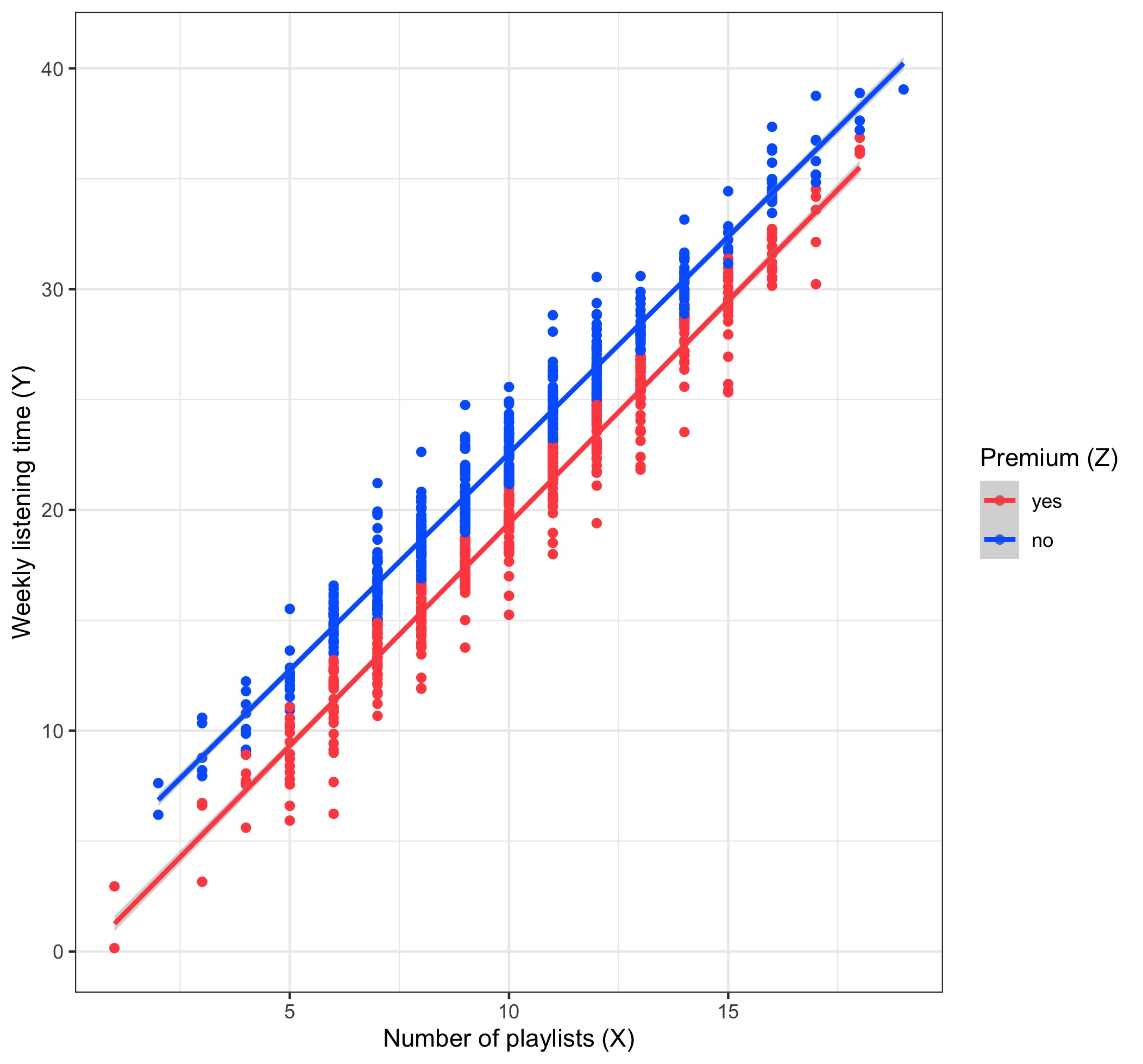
Let’s say you’re working for an online music streaming service that recently introduced a paid premium subscription service that allows members to listen to music ad-free. The premium account model was rolled out a few months ago and you wish to assess its impact on the listening habits of users. You dig into the logs collected by the service and you find something disturbing: it looks like subscribing to the premium account reduces (rather than increases) the listening time, adjusting for the number of playlists a user has created. At the next team meeting, you present the following plot:
You explain that you ran the regression
and found that the causal effect of signing up for a premium account is hours of the member’s weekly listening time. What’s worse is that this estimate is statistically significant from !
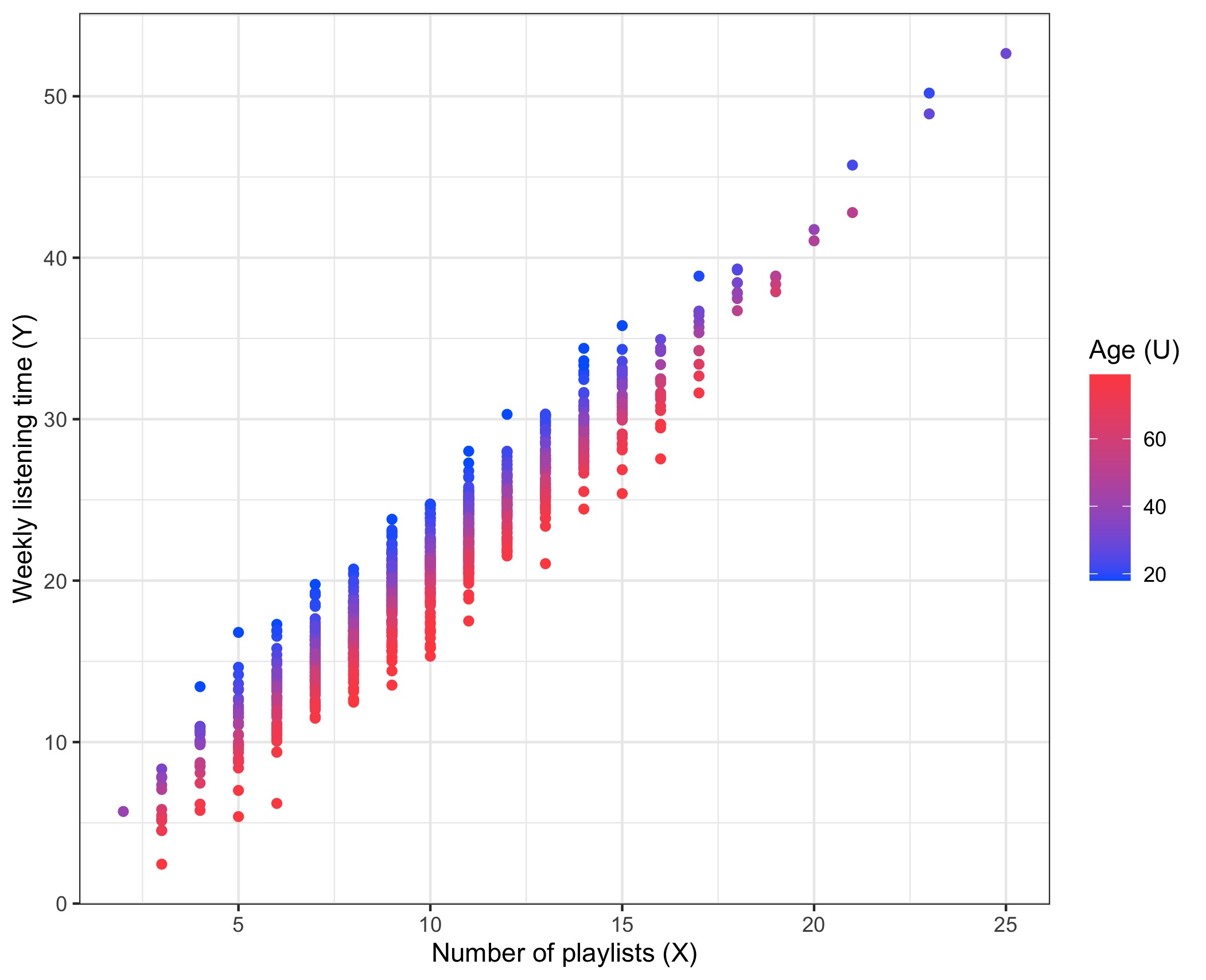
Thankfully one of your colleagues points out that among users with any given number of playlists (), older ones are both more likely to be premium subscribers, and also likely to spend less time listening to music than younger users: in other words, age is likely to be a confounder! Indeed, you dig a little more and plot against again, but this time you overlay the age :
Which lends support to your colleague’s suspicion. In fact, we know the ground truth (since, well, this is a fictional example and we generated the data!). Indeed, the data was generated so that ; that is, the membership has absolutely no effect on the listening time!
Clearly, ‘‘just running a regression’’ did not work out so well. Perhaps those causal folks are onto something.
A second example
One of your teammates working on the infrastructure noticed your plot and was very interested. Indeed, the infrastructure team is having a hard time figuring out how quickly they should increase their streaming capacity: too quickly and they are wasting money; too slowly and they are providing suboptimum bandwidth to the users. Based on your plot, she wonders whether she could use the number of playlists () and the premium membership status () to predict the amount of streaming time per user (), which would be helpful in calibrating the bandwidth. Having learnt your lesson, you flattly assert that regressions are evil, and that nothing good can come off it.
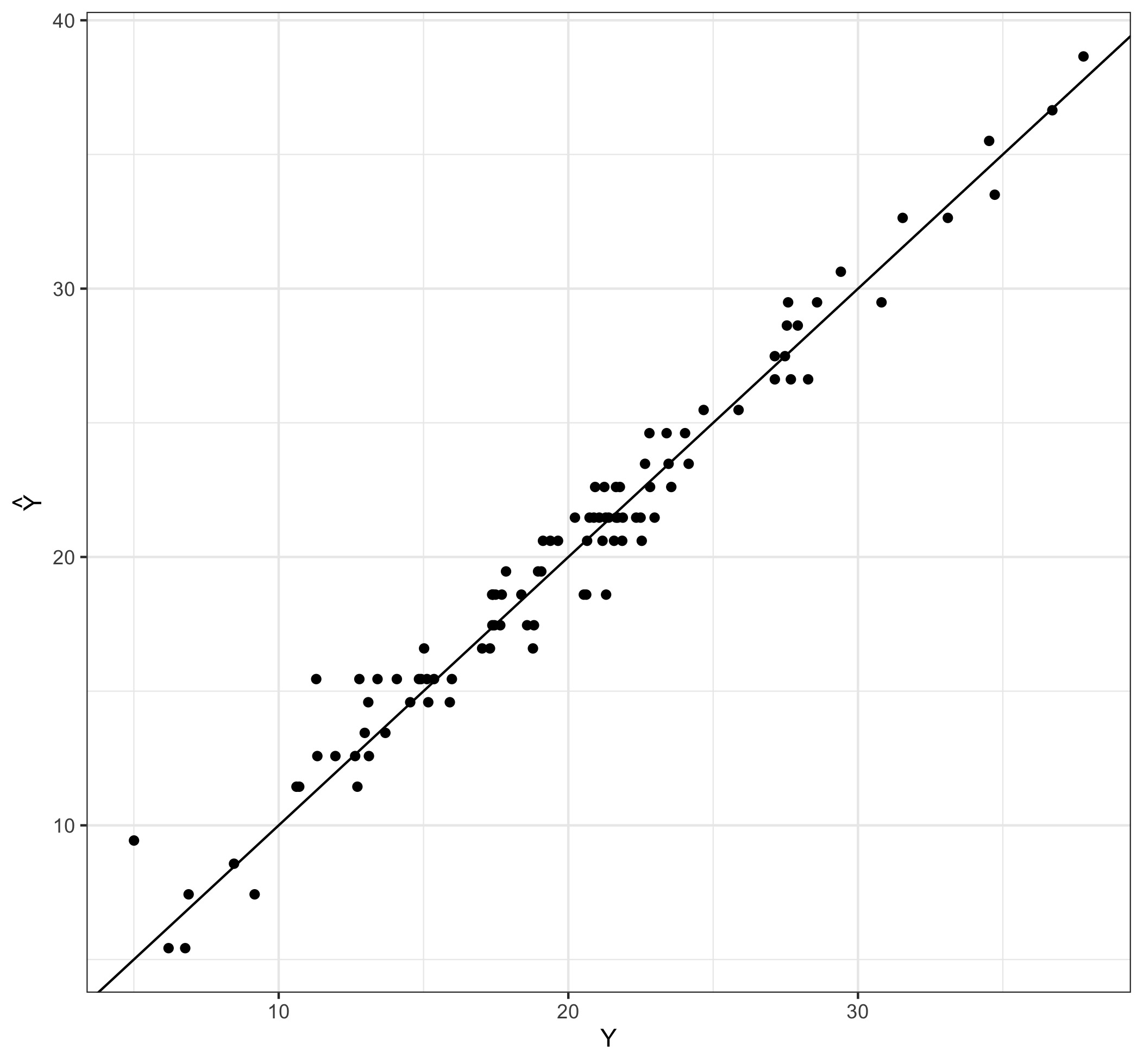
Your colleague is persistent though. She fits the regression on the available data, then waits patiently for new data to come in to checks her predictions against those new observations; the results are displayed in the Figure below.
Well, ‘‘sorry dude but it just works,’’ she says, as she goes back to her office to use her predictions to improve the infrastructure.
You scratch your head in confusion… so regression works?
Correlation vs Causation
What happened?
So, what happened there? In the first example, regression gave us the wrong answer; in the second example, it gave us the right answer. Why?
Well, in the first example, you asked a causal question: what would be the causal effect of giving everyone a premium subscription. As we saw in our previous post , answering such questions with observational data (as opposed to data from a randomized experiment) requires care: in particular, it requires that one adjust for all confounders (we will discuss observational studies in more details in another post).
The second example, however, has nothing to do with causal inference: we asked a purely predictive question. Now, of course, you still need to be mindful of the usual prediction challenges (e.g. the bias-variance tradeoff, overfitting, etc…), but unmeasured confounders have no special role here.
Takeaway
So can you ‘‘just run a regression’’? It depends on the type of question you’re asking. If you’re asking a causal question, then you should be worrying about unmeasured confounders (among other things); if you’re asking a predictive question (or indeed, a simple descriptive question), then you can use your usual tools without being paranoid about unmeasured confounders.